命題15
もし、立方数が立方数を割り切るならば、そのとき、その辺もまたその辺を割り切り、また、その辺がその辺を割り切るならば、そのとき、その立方数もまたその立方数を割り切る。

立方数Aは立方数Bを割り切るとし、CをAの辺、DをBの辺とせよ。
CはDを割り切ると主張する。
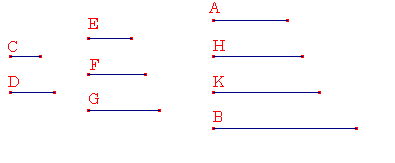
Cにそれ自身をかけてEを作り、Dにそれ自身をかけてGを作り、CにDをかけてFを作り、CとDにFをかけて、おのおのHとKを作るとせよ。
今、E、F、GとA、H、K、Bは、CがDに対する比と連続して比例することは明白である。
また、A、H、K、Bが連続して比例し、AはBとGを割り切るので、それゆえに、AはHを割り切る。propositionⅧ11、propositionⅧ12
また、AはHに対して、CはDに対する。propositionⅧ7
それゆえに、CもまたDを割り切る。definitionⅦ20
次に、CがDを割り切るとせよ。
AもまたBを割り切ると主張する。
同じ作図があれば、同様にしてA、H、K、Bは、CはDに対する比で連続して比例することは証明できる。
また、CはDを割り切り、CはDに対して、AはHに対するので、それゆえに、AもまたHを割り切り、つまり、AはBも割り切る。definitionⅦ20
それゆえに、もし、立方数が立方数を割り切るならば、そのとき、その辺もまたその辺を割り切り、また、その辺がその辺を割り切るならば、そのとき、その立方数もまたその立方数を割り切る。
証明終了